Dispersion curve inversion

This tutorial shows how to invert a dispersion curve measured for surface waves. It is based on dinverdc module used inside dinver framework.

Getting ready

Start Dinver with Surface Wave Inversion module.

At first glance, the interface might look a little bit messy. If it is the first time you start dinver, you'd better close all windows until having an empty workspace. The various tools will be displayed one by one and explained in this tutorial, in a logical order.

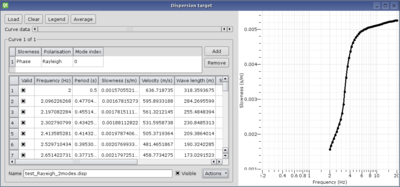
Importing the dispersion curve to fit

• Activate the Target panel in menu Tools.
• Select the Dispersion option. Leave the Misfit weigth and the Min. misfit to their default values, 1 and 0, respectively.
• Click on Set to load the dispersion curve, the Dispersion curve target is displayed.

Load a dispersion curve and fix its frequency sampling:

Loading a dispersion curve

• Load a dispersion curve from a text file (e.g. Test_Rayeigh_2modes.disp). It is a theoretical curve computed using tutorial Computing a theoretical dispersion curve.
• Select the fundamental curve

Use Curve data scroll bar and Visible button to identify it.

It is the curve defined over the complete frequency range and with higher slowness.

• Re-sample it from 2 to 20 Hz on log scale with 50 samples (menu Actions/Resample).
• Cut it from 2 to 20 Hz (menu Actions/Cut).
• Select the first higher mode curve

Use Curve data scroll bar and Visible button to identify it.

This curve is not defined over the complete frequency range and it has a lower slowness.

• Remove it (menu Actions/Remove).

Achieving a good frequency sampling is an art, for a better understanding see Curve sampling.

At this step, the Dispersion curve target should contain only one curve, the fundamental mode. Make sure the mode table contains only one item like this:

Fundamental mode ready for inversion

Defining the parameter space

Defining the parameter is the key point of the inversion. At this step you have to figure out what information you already know about the ground structure and information you would like to extract. More details on how to achieve a suitable parameterization.

• Activate the Parameter panel in menu Tools.
• Add two layers for Vp profile by clicking two times on Add button in Compressional velocity profile.
• Add one layer for Nu profile by clicking once on Add button in Poisson's ratio profile.
• Add two layers for Vs profile by clicking two times on Add button in Shear velocity profile.
• Add one layer for Rho profile by clicking once on Add button in Density profile.
• Link Vp interface to Vs interface by selecting Vs0 in Linked to combo box.

At this step, the parameterization describes a ground structure with one layer over a half-space with uniform Vp and Vs in the top and bottom layer. The default range for values is relatively large. Vp contrast is forced to be at the same depth of Vs contrast, and only one parameter for depth is kept. Poisson's ratio is not a parameter but a condition imposed to Vp and Vs values: computed Poisson's ratios must remain between 0.2 and 0.5 (usual values for soils and rocks). The parameter panel should look like this one:

Parameter panel for a very simple ground structure

Running the inversion

Run list and tuning parameters with default values

Before going any further, it is wise to save the current environment, i.e. the target and parameter space definitions into a .dinver file. Select menu File/Save as .... Target and parameterization defined here above are available within file Dinverdc_tutorial-1.dinver.

Add a new Run by using menu Runs/Add. All the created runs are listed in Runs tab with their NA tuning parameters: itmax, ns0, ns and nr. All actions of menu Runs apply only to the selected rows this table.

Initialization log

Upon run initialization the parameter space specified previously with the graphical interface is translated into parameters ranges and explicit conditions. A report is presented in Log tab. Each run has an individual dedicated log.

---------------------- List of parameters and conditions
Dimension of parameter space         = 5
200 < TopVp0 < 5000 m/s(323 bins)
       TopVp0 < TopVp1
       Poisson's ratio checked
200 < TopVp1 < 5000 m/s(323 bins)
       TopVp0 < TopVp1
       Poisson's ratio checked
150 < TopVs0 < 3500 m/s(316 bins)
       TopVs0 < TopVs1
       Poisson's ratio checked
1 < DVs0 < 100 m(462 bins)
150 < TopVs1 < 3500 m/s(316 bins)
       TopVs0 < TopVs1
       Poisson's ratio checked
TopRho0=2000 kg/m3

The number of bins for each parameter is calculated to ensure a minimum relative precision of 1% (discrete values on a log scale).

Starting the inversion and status

Current status of inversion process

Select run in Runs table and hit Start in menu Run. The Status pane shows the current advance of the inversion process. The minimum misfit achieved as a function of the number of generated models is plotted on the left. The table on the right displays among other information the minimum misfit and the number of model generated.

Viewing the results

There are three ways of plotting inversion of dispersion curves within Dinver. They are available in menu View, only the selected runs in Runs table are included in the plots.

Dispersions

Options for dispersion curve display

This is probably the first thing to look at when running the first inversion on dispersion curve. You can estimate whether the best models have a dispersion close to the inverted curve. Select the correct slowness (phase or group) and polarization (Rayleigh or Love). All models with a misfit lower or equal to Maximum misfit are displayed. Maximum number of modes is used only when several modes (fundamental and higher) are inverted together. In this case, the dispersion curve has no standard deviation, hence the misfit is normalized by the slowness value. A 10% fit of the dispersion correspond to a misfit of approximately 0.1.

Ground profiles

A similar dialog box pops up when viewing the ground profiles. Maximum number of profiles must be set to 2 for Vp and Vs. This must not be confused with the number of models displayed. This later is controlled only by the maximum misfit (suggested value: 0.1, see previous section).

Results for a dispersion curve inversion with a 2-layer model. Plots from dispersion curves and ground profile are merged in a single graphic sheet

Obviously, the dispersion curve is not perfectly fitted at high frequency due to the too simplistic parameterization used in this tutorial. To go further, more complex parameterizations are required.

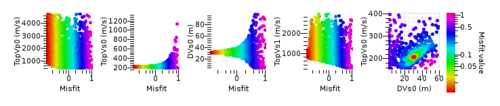
Parameter space projections

Under menu View, option Parameter space displays various 2D projections of the models. The default plots are parameter versus misfit values. Existing plots can be customized through the property editor or new plots can be inserted (menu Insert/Parameter plot.

Some parameter space projections

Checking the robustness

The inversion process is a random process based on a pseudo-random generator. The exploration paths covered may slightly vary from run to run (keeping everything else constant), especially in complex parameter spaces with a high number of dimensions. This is good practice to check the robustness of the exploration by starting the inversion with another seed. Add a new Run, select it in the Runs table and start it.

Comparison of minimum misfit achieved for three runs with distinct seeds

In this too simple parameterization (5 dimensions) the solution region is pretty well explored and a very similar misfit is achieved in all cases. At this scale (1e-7), the misfits can be identical due to the discrete nature of the inversion algorithm. A complete and reliable solution to the inversion problem require testing more complex parameterizations.