Difference between revisions of "Smoothing details"
Jump to navigation
Jump to search
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | The Konno and Ohmachi (1998) smoothing | + | The Konno and Ohmachi (1998) <ref name="Konno and Ohmachi (1998)">Konno, K. and Omachi, T., 1998, Bull. Seism. Soc. Am., 88, 228-241.</ref> smoothing is defined by the following function: <!--[[Image:Konno_Ohmachi_formula.png|100px]]--> |
| + | <math>\left(\frac{\sin(b\log_{10}(\frac{f}{f_c})}{b\log_{10}(\frac{f}{f_c})}\right)^4</math>, where: | ||
| − | *f is the frequency | + | * <math>f</math> is the frequency |
| − | * | + | * <math>f_c</math> is the central frequency |
| − | *b is the bandwidth coefficient. | + | * <math>b</math> is the bandwidth coefficient. |
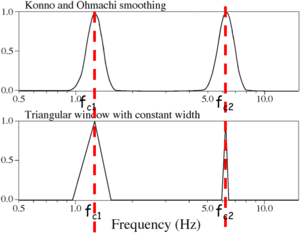
| − | + | Konno and Ohmachi smoothing function is strongly recommended for frequency analysis because it ensures a constant number points at low and high frequency. | |
| + | [[Image:Konno_Ohmachi_vs_triangle_smoothing.png|thumb|center|300px|Comparison between ''Konno and Ohmachi'' and triangular window smoothing.]] | ||
| − | + | == References == | |
| + | <references/> | ||
Latest revision as of 16:22, 14 April 2012
The Konno and Ohmachi (1998) [1] smoothing is defined by the following function: , where:
- is the frequency
- is the central frequency
- is the bandwidth coefficient.
Konno and Ohmachi smoothing function is strongly recommended for frequency analysis because it ensures a constant number points at low and high frequency.
References
- ↑ Konno, K. and Omachi, T., 1998, Bull. Seism. Soc. Am., 88, 228-241.