Difference between revisions of "Computing a theoretical dispersion curve"
(New page: Category:Tutorials) |
|||
| Line 1: | Line 1: | ||
[[Category:Tutorials]] | [[Category:Tutorials]] | ||
| + | |||
| + | This tutorial details all the steps needed to compute a dispersion with '''gpdc'''. | ||
| + | |||
| + | == Creating a model file == | ||
| + | |||
| + | Crete a text file (e.g. "test.model"): | ||
| + | |||
| + | # My first model: two layers over a half-space | ||
| + | # First line: number of layers | ||
| + | 3 | ||
| + | # One line per layer: | ||
| + | # Thickness(m), Vp (m/s), Vs (m/s) and density (kg/m3) | ||
| + | 7.5 500 200 1700 | ||
| + | 25 1350 190 1900 | ||
| + | # Last line is the half-space, its thickness is ignored but the first column is still mandatory | ||
| + | 0 2000 1000 2500 | ||
| + | |||
| + | All lines beginning with '#' are considered as comments and they are ignored. Several models can be chained in one single file, but no comment line is allowed between layers. Column separators can be either TAB or SPACE. The number of consecutive separators does not matter. | ||
| + | |||
| + | == Computing the dispersion curves == | ||
| + | |||
| + | To get the dispersion curve of Rayleigh fundamental mode: | ||
| + | |||
| + | gpdc test.model | ||
| + | |||
| + | You get as output: | ||
| + | |||
| + | # My first model: two layers over a half-space | ||
| + | # First line: number of layers | ||
| + | # One line per layer: | ||
| + | # Thickness(m), Vp (m/s), Vs (m/s) and density (kg/m3) | ||
| + | # Last line is the half-space, its thickness is ignored but the first column is still mandatory | ||
| + | # 1 Rayleigh dispersion mode(s) | ||
| + | # CPU Time = 1 ms | ||
| + | # Mode 0 | ||
| + | 0.2 0.00107882203003697 | ||
| + | 0.209523150557933 0.00107913814934707 | ||
| + | [...] | ||
| + | 19.0909691332367 0.00533451456923106 | ||
| + | 20 0.00533094289276869 | ||
| + | |||
| + | To compute Rayleigh higher modes (4 in this case) as well as the fundamental mode: | ||
| + | |||
| + | gpdc test.model -R 5 | ||
| + | |||
| + | To compute Love higher modes (4 in this case) as well as the fundamental mode: | ||
| + | |||
| + | gpdc test.model -R 0 -L 5 | ||
| + | |||
| + | To compute Love modes, you must set explicitly the number of Rayleigh to 0, it is one by default. | ||
| + | |||
| + | == Saving the dispersion curves == | ||
| + | |||
| + | gpdc test.model -R 2 > test_Rayeigh_2modes.disp | ||
| + | |||
| + | == Plotting the dispersion curves == | ||
| + | |||
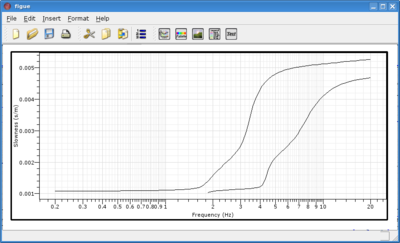
| + | We use '''figue''' to plot couples of values (X, Y), additionally we provide a '''make-up''' file to get the correct type and labeling of axes. Before running the next command you can download [dc.mkup]. | ||
| + | |||
| + | gpdc test.model -R 5 | figue -c -m dc.mkup | ||
| + | |||
| + | [[Image:gpdc_dispersion_plot.png|thumb|right|400px|Dispersion curve plot with figue]] | ||
| + | |||
| + | == Going further == | ||
| + | |||
| + | === Help about command line options === | ||
| + | |||
| + | To get help about all options: | ||
| + | |||
| + | gpdc -h all | ||
| + | |||
| + | === Programming interface === | ||
| + | |||
| + | The computation of dispersion is implemented in ''libqtbwave.so'' (or equivalent for Windows and Mac). You can access it through various languages: C++, C or Fortran | ||
| + | |||
| + | A C++ example: | ||
| + | |||
| + | // 3-layer model initialization | ||
| + | QtbLayeredModel model(3); | ||
| + | model.h()[0]=7.5; | ||
| + | model.h()[1]=25.0; | ||
| + | model.slowP()[0]=1.0/500.0; | ||
| + | model.slowP()[1]=1.0/1350.0; | ||
| + | model.slowP()[2]=1.0/2000.0; | ||
| + | model.slowS()[0]=1.0/200.0; | ||
| + | model.slowS()[1]=1.0/210.0; | ||
| + | model.slowS()[2]=1.0/1000.0; | ||
| + | model.rho()[0]=1800; | ||
| + | model.rho()[1]=1900; | ||
| + | model.rho()[2]=2500; | ||
| + | // Initialize frequency sampling, in angular frequency (omega)!! | ||
| + | QVector<double> x; | ||
| + | x.resize(50); | ||
| + | x[0]=...; | ||
| + | ...; | ||
| + | x[49]=...; | ||
| + | // Or use QtbCurve to generate linear or log series | ||
| + | QtbCurve<QtbPoint1D> c; | ||
| + | c.line( minFreq, 0.0, maxFreq, 0.0 ); | ||
| + | c.resample( nSamples, minFreq, maxFreq, Qtb::Log | Qtb::Function ); | ||
| + | c.multiply( 2*M_PI ); // convert to angular frequency | ||
| + | QVector<double> x = c.xVector(); | ||
| + | // Dispersion computation, fundamental mode only | ||
| + | QtbRayleigh modelRayleigh( &model ); | ||
| + | QtbDispersion dispersion( 1, &x); | ||
| + | dispersion.calculate( modelRayleigh, 0 ); // 0 is to avoid ellipticity computation | ||
| + | // Access computed values | ||
| + | QtbCurve<QtbPoint2D> * dc = dispersion.curve(0); | ||
| + | // See QtbCurve header for more information | ||
| + | // Or directly, fundamental mode, ith sample value. | ||
| + | dispersion.mode(0)[i] | ||
| + | |||
| + | |||
| + | === Theoretical considerations === | ||
| + | |||
| + | The equations and methods implemented in ''libqtbwave.so'' are fully described from a theoretical point of view in [http://marc.geopsy.org/publications.html Marc Wathelet's PhD thesis] (chapter 3). | ||
Revision as of 07:49, 24 July 2009
This tutorial details all the steps needed to compute a dispersion with gpdc.
Contents
Creating a model file
Crete a text file (e.g. "test.model"):
# My first model: two layers over a half-space # First line: number of layers 3 # One line per layer: # Thickness(m), Vp (m/s), Vs (m/s) and density (kg/m3) 7.5 500 200 1700 25 1350 190 1900 # Last line is the half-space, its thickness is ignored but the first column is still mandatory 0 2000 1000 2500
All lines beginning with '#' are considered as comments and they are ignored. Several models can be chained in one single file, but no comment line is allowed between layers. Column separators can be either TAB or SPACE. The number of consecutive separators does not matter.
Computing the dispersion curves
To get the dispersion curve of Rayleigh fundamental mode:
gpdc test.model
You get as output:
# My first model: two layers over a half-space # First line: number of layers # One line per layer: # Thickness(m), Vp (m/s), Vs (m/s) and density (kg/m3) # Last line is the half-space, its thickness is ignored but the first column is still mandatory # 1 Rayleigh dispersion mode(s) # CPU Time = 1 ms # Mode 0 0.2 0.00107882203003697 0.209523150557933 0.00107913814934707 [...] 19.0909691332367 0.00533451456923106 20 0.00533094289276869
To compute Rayleigh higher modes (4 in this case) as well as the fundamental mode:
gpdc test.model -R 5
To compute Love higher modes (4 in this case) as well as the fundamental mode:
gpdc test.model -R 0 -L 5
To compute Love modes, you must set explicitly the number of Rayleigh to 0, it is one by default.
Saving the dispersion curves
gpdc test.model -R 2 > test_Rayeigh_2modes.disp
Plotting the dispersion curves
We use figue to plot couples of values (X, Y), additionally we provide a make-up file to get the correct type and labeling of axes. Before running the next command you can download [dc.mkup].
gpdc test.model -R 5 | figue -c -m dc.mkup
Going further
Help about command line options
To get help about all options:
gpdc -h all
Programming interface
The computation of dispersion is implemented in libqtbwave.so (or equivalent for Windows and Mac). You can access it through various languages: C++, C or Fortran
A C++ example:
// 3-layer model initialization QtbLayeredModel model(3); model.h()[0]=7.5; model.h()[1]=25.0; model.slowP()[0]=1.0/500.0; model.slowP()[1]=1.0/1350.0; model.slowP()[2]=1.0/2000.0; model.slowS()[0]=1.0/200.0; model.slowS()[1]=1.0/210.0; model.slowS()[2]=1.0/1000.0; model.rho()[0]=1800; model.rho()[1]=1900; model.rho()[2]=2500; // Initialize frequency sampling, in angular frequency (omega)!! QVector<double> x; x.resize(50); x[0]=...; ...; x[49]=...; // Or use QtbCurve to generate linear or log series QtbCurve<QtbPoint1D> c; c.line( minFreq, 0.0, maxFreq, 0.0 ); c.resample( nSamples, minFreq, maxFreq, Qtb::Log | Qtb::Function ); c.multiply( 2*M_PI ); // convert to angular frequency QVector<double> x = c.xVector(); // Dispersion computation, fundamental mode only QtbRayleigh modelRayleigh( &model ); QtbDispersion dispersion( 1, &x); dispersion.calculate( modelRayleigh, 0 ); // 0 is to avoid ellipticity computation // Access computed values QtbCurve<QtbPoint2D> * dc = dispersion.curve(0); // See QtbCurve header for more information // Or directly, fundamental mode, ith sample value. dispersion.mode(0)[i]
Theoretical considerations
The equations and methods implemented in libqtbwave.so are fully described from a theoretical point of view in Marc Wathelet's PhD thesis (chapter 3).