Geopsy: Damping

Damping is an advanced signal processing toolbox originally aiming at computing the viscous damping ratio of an identified oscillating structure using the Random Decrement technique . It can also be very useful in identifying industrial vibration sources (rotating machines, etc.) that can affect and alter H/V and array analysis results.

Background

Spectrum of recordings in a building for which the damping will be calculated

Viscous damping ratio is a parameter representing the energy loss of an oscillating system. The loss can be either internal (material damping) or to another system (radiated damping). The computation of the viscous damping assumes the friction forces (energy loss) are proportional to the velocity of the system. For a single degree-of-freedom system, the solution of the differential equation in time (impulse response function) is then an exponentially decreasing sinus function of the form:

$h(t)=\alpha e^{-\xi \omega t}sin(\omega 't)$

with $\omega '=\omega {\sqrt {1-\xi ^{2}}}$, $\xi$ the damping ratio and $\omega$ the angular resonance frequency of the system. The assumption of viscous damping may not be appropriate in all cases but is common in civil engineering and seismology.

The Random Decrement technique is based on the assumption that at each time step, the signal is the sum of a random signal and the impulse response function of the study-system. Stacking many time windows with the same initial condition results in enhancing the impulse response function component with respect to the zero-mean random part. The algorithm selects all the windows of the given length starting with a 0 amplitude and a positive derivative and averages them. Then, the Impulse response function is fitted by an exponentially decreasing cosine function (starting at 0) depending on an amplitude $\alpha$, the resonance frequency $f={\frac {\omega }{2\pi }}$ and the damping ratio $\xi$.

Practical Use

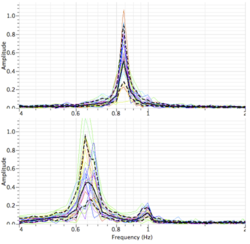
The Damping toolbox is used in Geopsy after detecting peaks in the Power Spectrum or the Structure spectrum. Computing the damping ratio is above all an indication on the origin of the peak. An undamped peak ($\xi <<1$) is produced by a self-entertaining source, generally an industrial machine. In an oscillating structure like a building, the damping ratio ranges between 1 and 10%. Slightly lower values are possible for slender structures. Higher damping cannot generally be detected in recordings because of too low energy. For ground ambient vibration recordings, oscillating structures (machines, buildings, trees...) may pollute the signals and lead to false interpretation, e.g. of the H/V spectral ratios.

Damping toolbox pop-up menu

Damping ratio toolbox

Starting the Damping toolbox found in the Menu Tools or using the Toolbar applies the Random Decrement technique to the signals in the active signal viewer.

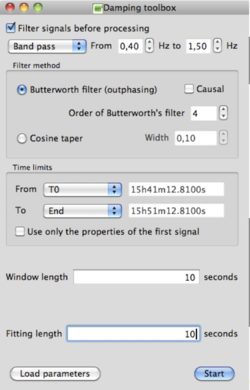
The Damping toolbox is divided into 3 parts: Filter, Time Limits and Parameters of the Random Decrement technique. These parameters are automatically saved and can be restored clicking on Load Parameters.

Filter

Filtering can be activated by checking Filter signal before processing. Applying a narrow band filter is generally necessary in order to select the frequency band of the interesting peak, since other peaks are generally existing in the spectrum. This may strongly affect the signals and is the major drawback of the random decrement technique. The available filtering options are detailed in Filter.

Time Limits

The time limits define the signal range on which the Random Decrement Technique is applied. Options for Time Limits are defined in the corresponding section.

Parameters of the Random Decrement technique

In Geopsy, two parameters can be customized to compute the damping ratio using the Random Decrement technique:

• Window length is size of the stacked windows to compute the random decrement. It should contain at least 10 periods, i.e. ${\frac {10}{f_{0}}}$ seconds, with $f_{0}$ the resonance frequency of interest.
• Fitting length is the time length of the resulting random decrement used for the fitting. It should therefore be lower or equal to the window length. It should first be set to the window length and eventually decreased if the end of the response function is no more described by an exponentially decreasing cosine function.

Several window lengths should always be tested in order to check the robustness of the results.

Damping results in each direction of the building. This structure has particularly small damping ratios.

Results

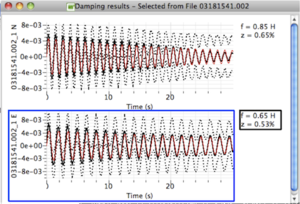
When clicking on start button, a results page appears with one graph per signal processed. Each graph includes 1 layer with 4 lines representing the mean (solid black line) and standard deviation (dashed black line) of the Random Decrement and the fitted exponentially decreasing function (solid red line). Next to each graph, the frequency f (in Hertz) and damping ratio z (in %) of this fitted function are displayed.